Structural Analysis - Experimental Covariance

Structural analysis and experimental covariance are fundamental tools for understanding the behavior of regionalized variables. In this article, we use the lagged scatter plots to explore the spatial relationship of a variable at different distances.

Remember that the lagged scatter plot is a graph that compares the variable Y(x) with its displaced version, Y(x+h). This displacement allows us to evaluate the spatial correlation as we move away from a given position. For each value of h, we calculate the covariance between the original and displaced variable.

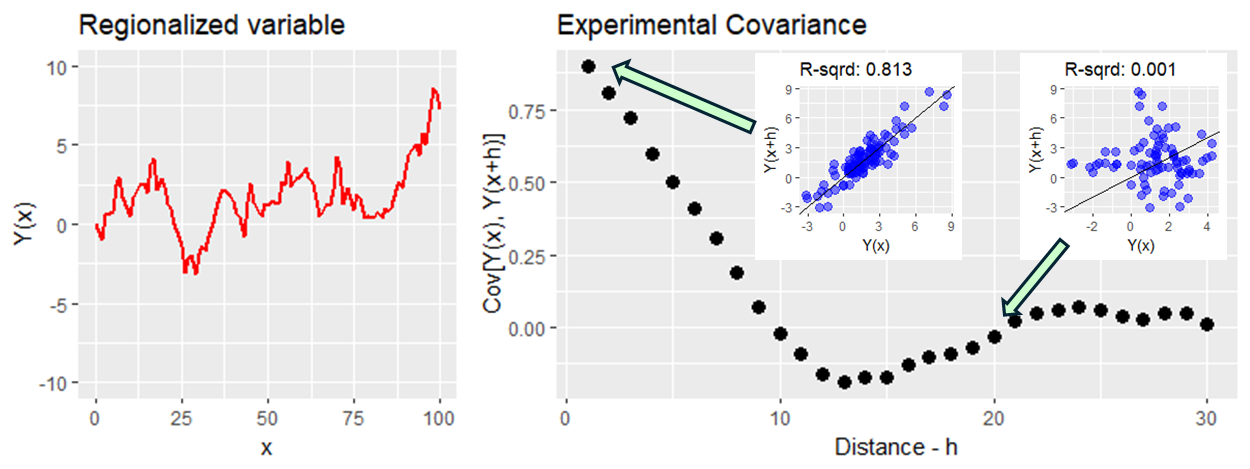
For a highly structured variable, such as in the case Y(x) = 0.99*Y(x-1)+e(x), we observe that the covariance gradually decreases as we move away from our reference position (Figure).

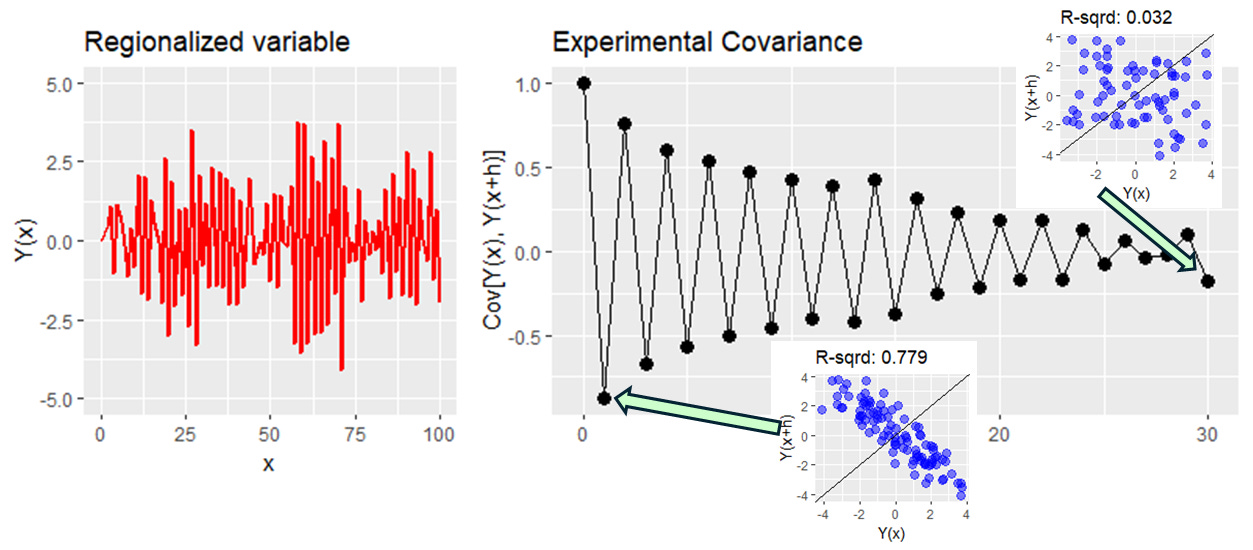
In contrast, for a variable with a negative structured component, such as:

Y(x) = -0.99*Y(x-1)+e(x)

The covariance tends to zero as we move away from a reference position but exhibits an oscillatory behavior (Figure).

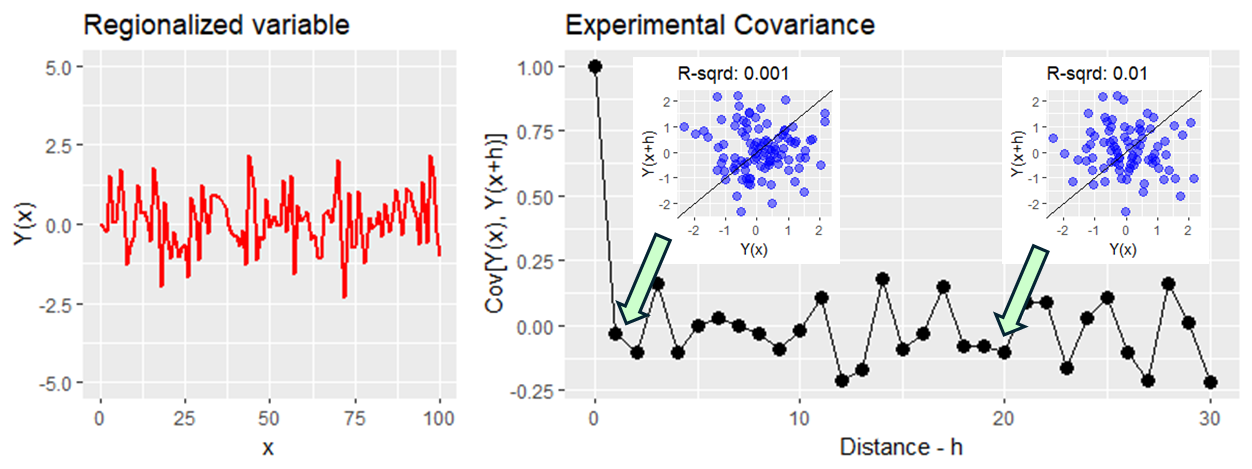
When we remove the structured component, as in the case of Y(x) = e(x), the covariance immediately drops to zero, regardless of the distance to the reference position (Figure).

This analysis shows how the covariance of a lagged scatter plot can be used to capture the spatial behavior of a regionalized variable. We will explore how these results can be applied in spatial attribute estimation in future publications. If you would like more information on these concepts or to apply them to your project, feel free to contact us at contacto@m2p.cl.

References:

Armstrong, M., Basic Linear Geostatistics, 1998, Springer Berlin Heidelberg.

Emery, X., 2013. Geoestadística. Universidad de Chile, Santiago, Chile.